https://dalekiewidoki.pl/refraction_calc – Atmospheric Refraction Coefficient Calculator – calculate the atmospheric refraction coefficient at which point C is visible from point A exactly behind point B.
https://dalekiewidoki.pl/range_calc – Visibility Range Calculator – calculate the maximum visibility range considering Earth’s curvature and atmospheric refraction.
Introduction
If Earth didn’t have an atmosphere, light would travel in a straight line, making it impossible to carry out many distant observations. What enables observations over much greater distances than usual is atmospheric refraction, which is the bending of light in the air. A distant view of a specific object is not always possible because the curvature of the Earth and obstacles between the observer and the observed object come into play.
But is it possible to peek beyond the horizon and „overcome” these obstacles?
Yes, we need increased atmospheric refraction, or a stronger than usual „bending” of light for that. To know when this stronger bending occurs, we need to start with some theory.
Refraction coefficient
Atmospheric refraction depends on the vertical temperature gradient, i.e., the rate at which temperature changes with altitude. Changes in atmospheric pressure with increasing altitude also affect refraction. To describe this phenomenon, a refraction coefficient is used. The higher the refraction coefficient, the stronger the „bending” of light, allowing one to „see farther.” The index in question is the ratio of the Earth’s curvature radius to the light path radius.
In programs simulating the effect of refraction on visibility, the following assumption is used – mathematically, the effect of atmospheric refraction is as if light travels in a straight line, and the Earth has a radius equal to r = R / (1 – k), where R is the radius of the Earth, and k is the refraction coefficient.
You can calculate refraction coefficient local value using an appropriate formula.
where k- refraction coefficient P – atmospheric pressure in hPa, T – air temperature in kelvins, dT / dh – vertical temperature gradient per 1-meter height difference (in K/m).
You can calculate the index using a spreadsheet from the Dalekie Horyzonty website. You can find its derivation, for example, on this page. It’s a simplified formula that doesn’t consider factors that have a minimal impact on refraction, such as air humidity.
What values can the refraction coefficient take?
The value of the standard refraction coefficient is considered to be 0.13 – 0.14.
Theoretically, locally, the refraction coefficient can exceed a value of 1.0 – this is called „superrefraction”. In such a case, it would be possible to see everything far away on Earth, regardless of the Earth’s curvature. Everything above the layer where superrefraction occurs would be visible, provided visibility conditions like air transparency (pollution, aerosol concentration, etc.) allow for it.
Atmospheric Refraction and Long-Distance Photography
Long-distance photography aims to capture objects from a great distance. Typically, such photographs are taken under standard conditions because they are most common. To capture an object from a distance, „only” good visibility and air transparency are often enough. Standard refraction (with a coefficient of 0.13) is sufficient, for example, for observing the Slovak Tatra Mountains from a distance of over 200 km from Poland or Andes from the Cordoba region in Argentina at a distance of 440 km.
However, there are more challenging observations – extreme long-distance observations. Extreme not only because of the distance from the observed object but also because of the difficulty of observation, such as terrain profile and obstacles. For such observations, increased atmospheric refraction is needed to allow the detection of an object „hidden” beyond the horizon. You can find many such photos on the dalekiewidoki.pl website.
Extreme Observations of the Tatras from Poland
Let’s start with a review of Tatra observations. The Tatras are the highest (maximum 2655 meters above sea level) mountain range in the Carpathians and the highest between the Alps and the Urals and the Caucasus. This mountain range was observed from Central and Eastern Poland from a distance of over 230 km, with a required refraction coefficient of over 0.20.
Let’s move on to some examples. Let’s start with observations of the Slovak Tatras from G. Kamieńska (Central Poland) at a distance of 232 km. The required refraction coefficient for observing a single Tatra peak was 0.19. During the observation, the refraction coefficient for the visible part of Gerlach was about 0.23.
You can find a full report on the dalekiewidoki.pl website. Calculations of refraction for this observation can be found in an article on Dalekie Horyzonty.
Line of sight from G. Kamieńsk to Gerlach. 232.1 km on Google Maps.
The next example is the observation of the Tatra Mountains from the Lublin Upland from a distance of 233 km. From the point in the village of Potok Wielki, located at only 245 meters above sea level, the atmospheric refraction coefficient required to observe the part of Zadni Gerlach (2616 meters above sea level) visible in the photo was approximately 0.22.
Observations of objects at lower altitudes and the influence of radiation inversion.
Observations of objects at lower altitudes, where the line of sight is close to the ground, are more susceptible to the effects of refraction than observations of high mountains, where light travels a greater distance above the ground. This is due to radiation inversion, which occurs in a thin layer near the ground during clear and calm weather conditions, especially at night. This layer cools faster than the air above, leading to a large temperature gradient and an increased refractive index.
Let’s move on to examples of such observations.
Warsaw from the Holy Cross Mountains.
An observation that made headlines in the nationwide media was a photograph of the capital of Poland, Warsaw, taken from the Holy Cross Mountains from a distance of over 150 km.
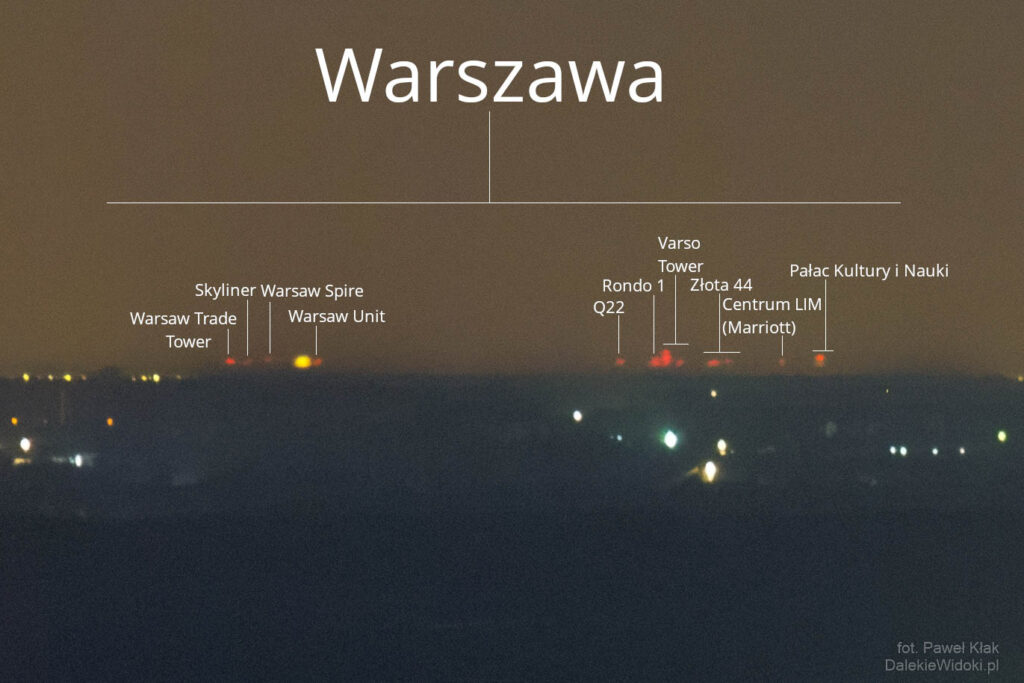
The changing atmospheric refraction over time caused the Warsaw skyscrapers to appear and disappear above the horizon. At the peak moment, the refraction was so strong that the building – Centrum LIM – was visible in the photo. This required a refraction coefficient of 0.44, which means that the light had to bend three times more strongly than usual. Due to the atmospheric inhomogeneity, we are talking about averaged coefficients for the entire observation distance.
In standard conditions (refraction coefficient ~ 0.14), to see the top of the Centrum LIM mast, the building would have to be about 190 meters taller, or you would need to rise over 360 meters above the observation point.
Importantly, the strong refraction and radiational inversion required for this observation are confirmed by official data available from the Legionowo station at 2:00 AM on May 28, 2023, which originate from a meteorological balloon used for atmospheric sounding.
In Legionowo, a temperature inversion occurred at altitudes ranging from 104 to 203 meters above sea level, which is approximately 10 to 110 meters above the Earth’s surface (likely extending slightly higher, as the temperature was the same at altitudes of 203 and 228 meters above sea level). We do not have data from the Warsaw – Łysa Góra route, so it is impossible to precisely determine the distribution of this coefficient along the entire observation line. Nevertheless, the weather conditions were similar, so there was probably also an inversion there. The line of sight only passed through the inversion layer for part of the route, which is why the average refraction coefficient is significantly lower than its maximum values. The lowest visible object in Warsaw in the photos is the light on the mast of the Centrum LIM building, which reaches a height of 295 meters above sea level.
Using specialized software that analyzes how light propagates through the atmosphere, taking into account a specific vertical temperature profile, we can determine the line of sight under given conditions.
The charts presented below were prepared by Dr. Hab. Krzysztof Strasburger based on measurements conducted in Legionowo. A detailed description can be found on his website.
Warsaw from the vicinity of Łódź.
Another interesting observation is the photos of Warsaw taken from the vicinity of Łódź are presented in an article. Let’s analyze this observation in terms of non-standard atmospheric refraction.
A few minutes later, the changing refraction revealed its beauty. Many more objects of Warsaw appeared.
On the horizon, several skyscrapers of Śródmieście and Wola appeared: Warsaw Trade Tower, Warsaw Spire, Spektrum Tower, Łucka City, Generation Park, Mennica Legacy Tower, Skysawa, Unit, Skyliner, Rondo 1, The Warsaw Hub, Złota 44, Palace of Culture and Science, Varso Tower, LIM Center (Marriott), Chałubińskiego 8, as well as much lower structures such as the control tower (TWR) of Chopin Airport in Warsaw.
Course of the Kalenice – Warsaw line of sight.
Observer: Kalenice, Łódź Voivodeship, from a point near the forest near the A2 motorway, altitude 166 meters above sea level. 51°57’47.7″N 19°51’22.7″E
Observed object: Control tower (TWR) of Chopin Airport in Warsaw – altitude 153 meters above sea level. 52°09’44.6″N 20°57’34.5″E
Distance: 78.6 km
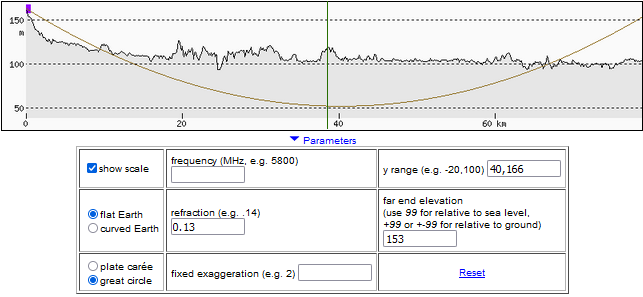
The illustrations below show the course of the Warsaw line of sight (Chopin Airport control tower) from Kalenice, Łódź, and were created using the heywhatsthat.com program.
They show how the terrain along the observation line would obstruct the view if light traveled in a straight line, as well as during standard atmospheric refraction.
Terrain profile with real proportions and Earth’s curvature – terrain height differences are too small relative to the observation distance to make the profile legible.
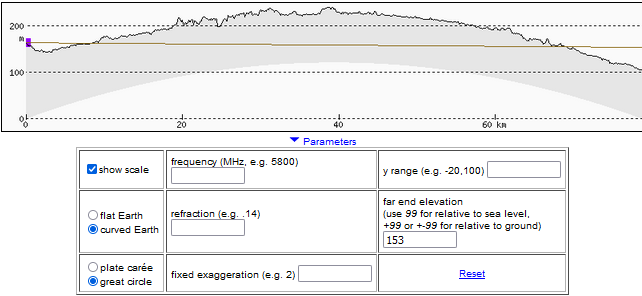On this profile, we have the line of sight without refraction – it would be as if the Earth had no atmosphere. To improve clarity, the profile is stretched vertically.
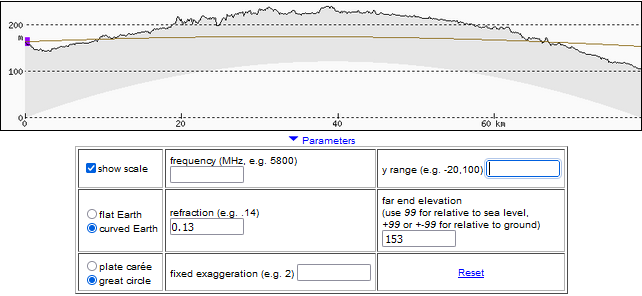Profile for standard atmospheric refraction (refraction coefficient 0.13). Visibility is still not possible – the line intersects several elevations. We see that the terrain would have to be about 80 meters lower for visibility to be possible with standard refraction.
To improve clarity, we stretch the profile vertically and transform it in such a way that the Earth’s surface is straightened, and its curvature is precisely represented by the curvature of the line of sight. Only the reference frame changes, the course of the line relative to the terrain remains the same. This profile shows the line of sight with standard refraction.
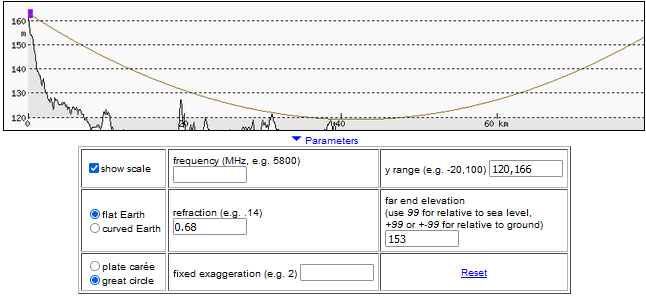We increase the refraction coefficient to 0.68, and now the line runs above the terrain along the entire observation distance.
Determining the minimum refraction coefficient required for observation
Let’s use the functionality of the heywhatsthat.com program. However, we need some important data about the observation.
In the photo, lights of the Chopin Airport control tower can be seen minimally protruding above the horizon. Knowing their height (153 meters above sea level), the observation point’s height (166 meters above sea level), and the height of the trees over which they can be seen, we can estimate how significant atmospheric refraction was. The location of the trees and their height are read from the NMPT model in Geoportal, using the terrain profile on heywhatsthat.com (description of the method) – it is about 130-140 meters above sea level for the trees of the Bolimowskie Forest near Żyradow and the point 52.062318 20.396667. For calculations, let’s assume a value of 135 meters above sea level.
Measurement of tree heights in the Bolimowskie Forest, which in standard conditions obscure Warsaw (Geoportal)
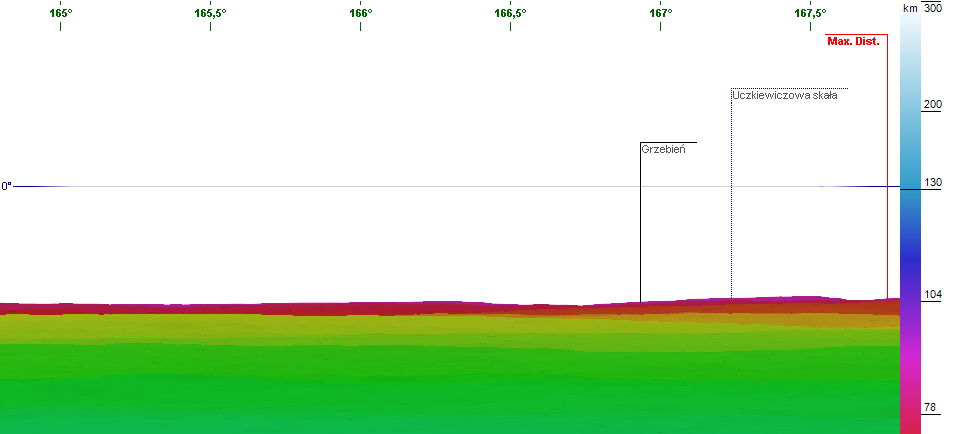
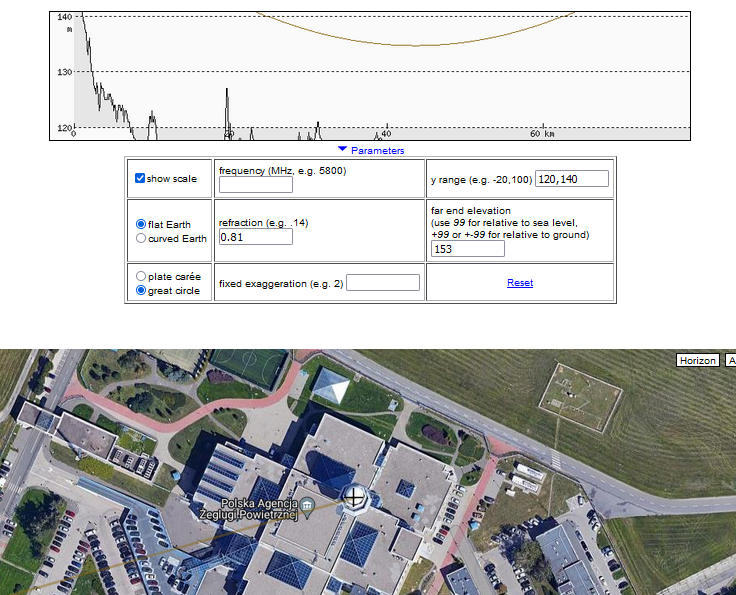Line of sight of the control tower (TWR) of Chopin Airport in Warsaw from Kalenice near Łódź on the terrain profile (heywhatsthat.com/?view=G14GDX81). For refraction coefficient 0.81, the line of sight passes through the location of trees at about 135 meters above sea level. The „flat earth” function in this program is intended to improve clarity; the Earth’s surface is straightened, and its curvature is precisely represented by the curvature of the line of sight. Only the reference frame changes, and the course of the line relative to the terrain remains the same.
On the terrain profile in heywhatsthat.com, the line of sight passes through the location of these trees at about 135 meters above sea level when the refraction coefficient is about 0.81. Similar values also result from the analysis of the visibility of other buildings.
Let’s now check the refraction coefficient required for the observation of the Marynarska Business Park.
Calculation of the refraction coefficient.
You can calculate it using the spreadsheet, in which you provide the elevation above sea level of the observation point, the height of the observed peak, the farthest visible point before this peak, and the distance from the observation point to both of these points.
This spreadsheet uses the fact that at the minimum refraction required for visibility, all three of these points lie on a common circle – the calculations involve finding its radius and then dividing by the radius of the Earth. A detailed description of the equations used can be found on the Calculations page.
The refraction coefficient required for the observation of the Marynarska Business Park is approximately 0.80.
Averaged refraction coefficient does not fully reflect the dynamics of refraction along the entire line of sight. Refraction varies over time and at different altitudes. Undoubtedly, at some distance of observation, the coefficient exceeded 1. However, it is not possible to assign a single value of refraction for the entire line of sight. The averaged refraction coefficient provides an overview of the observation difficulty and the strength of refraction needed for an object to „emerge” from beyond the horizon and be visible.
We were dealing with radiative refraction. Light traveling through a non-uniform atmosphere bent strongly due to „diving” into the near-surface inversion layer. In this layer, superrefraction likely occurred, and the refraction coefficient could have exceeded 1. In such a case, theoretically, it was possible to see everything anywhere on Earth that protruded above this layer, provided that visibility conditions such as air transparency, dust, and aerosol concentration allowed it.
The result of the strong bending was the deformation of the image of skyscrapers, i.e., flattening of objects and dynamic changes in their angular sizes over a relatively short period.
Importantly, radiative inversion and increased refraction required for such observations are confirmed by official data from the nearby Legionowo station at 2:00 AM on June 27, 2023, which is 3 hours after the observation. The data comes from a meteorological balloon used for atmospheric sounding.
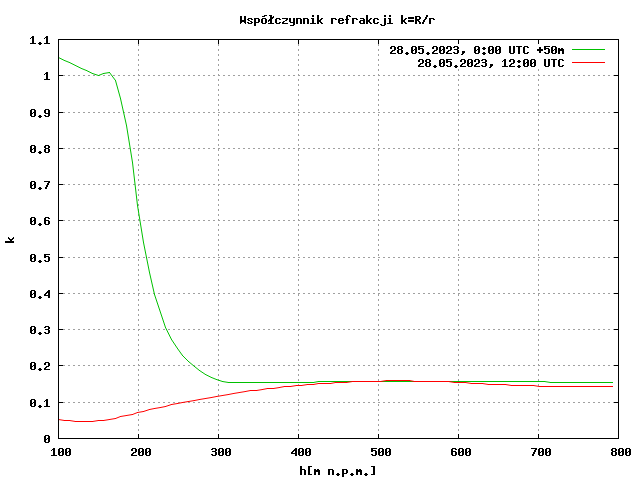
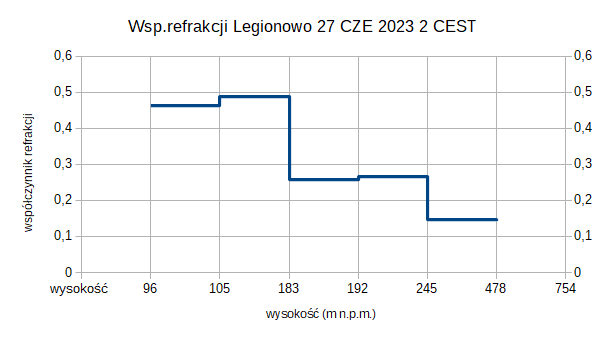Refraction coefficient chart based on data from Legionowo. The line has a step-like character due to the small number of measurement points – it represents average values of the coefficient between points. In reality, the refraction coefficient changes smoothly, and between 105 and 183 meters above sea level, it was highest.
The temperature inversion in Legionowo occurred at altitudes ranging from 96 to 245 meters above sea level, i.e., a maximum of about 160 meters above the ground, and the average value did not exceed 0.5.
A 3-hour interval is quite a long time, which explains the difference in the refraction value calculated for objects visible from Kalenice and the one calculated for Legionowo. The inversion layer could change even within a few minutes, which was evident in the photos. It is not possible to determine the exact distribution of this coefficient along the line of sight because these are not data from the Warsaw-Kalenice line. What we can draw from the data from Legionowo is not the strength and value of refraction but the fact of the appearance of inversion in the area.
