Obliczenia refrakcji atmosferycznej.
Wstęp
Fotografia długodystansowa ma na celu uchwycenie obiektów z możliwie najdalszego dystansu. To, co umożliwia obserwacje na znacznie większe dystanse niż te które wynikałyby z kalkulatorów zasięgu widoczności dla kulistej Ziemi pozbawionej atmosfery to refrakcja atmosferyczna czyli załamanie światła w powietrzu. Daleki widok konkretnego obiektu nie zawsze jest możliwy, gdyż na przeszkodzie stoi krzywizna Ziemi oraz przeszkody występujące pomiędzy obserwatorem a obserwowanym obiektem. Czy jednak da się zajrzeć dalej niż zwykle za standardowy horyzont? Tak. Potrzebujemy do tego zwiększonej refrakcji atmosferycznej czyli silniejszego niż zwykle „ugięcia” światła. Aby wiedzieć kiedy to silniejsze załamanie występuje musimy zacząć od teorii.
Współczynnik refrakcji.
Załamanie światła mierzymy posługując się współczynnikiem refrakcji atmosferycznej. Im wyższy współczynnik tym załamanie światła jest mocniejsze i w konsekwencji można widzieć dalej. Wartość współczynnika refrakcji uznawana za standardową w środkowoeuropejskim klimacie to 0,13-0,14. Taką też wartość za standardową podają programy do generowania panoram i zasięgu widoczności – heywhatsthat.com udeuschle.de oraz peakfinder.com. W większości przypadków podczas dalekich obserwacji spotykamy się z wystąpieniem właśnie takiej refrakcji.
Możemy za pomocą różnych danych wyliczyć lokalną wartość współczynnika refrakcji oraz średnią wartość tego współczynnika wymaganą do widoczności określonego punktu.
- Lokalna wartość współczynnika refrakcji.
Lokalną wartość współczynnika refrakcji możemy obliczyć przy pomocy poniższego wzoru którego wyprowadzenie znajdziemy na tej stronie. Wykorzystujemy do tego dane pomiarowe pochodzące z balonu meteorologicznego wykorzystywanego do sondowania atmosfery dostępne np. na stronie weather.uwyo.edu lub dane z prognozowanych radiosondaży np. z aplikacji Windy.
![]()
gdzie P – ciśnienie atmosferyczne w hPa, T – temperatura powietrza w kelwinach, dT / dh – pionowy gradient temperatury na 1 m różnicy wysokości (w K/m).
Widzimy , że kluczowe dla wzrostu współczynnika refrakcji jest wzrost gradientu temperatury w °C na 100 m oraz ciśnienia oraz spadek temperatury.
- Średni współczynnik refrakcji atmosferycznej wymagany do widoczności punktu.
Wartość uśrednionego współczynnik refrakcji potrzebną do zaobserwowania obiektu z punktu obserwatora z uwzględnieniem wysokości przeszkody pomiędzy tymi punktami, można obliczyć jako stosunek promienia krzywizny Ziemi do promienia krzywizny toru światła omijającego przeszkodę pomiędzy obserwatorem a obserwowanym obiektem.
W programach generujących widok oraz zasięg widoczność z określonego punktu , wpływ refrakcji na widok wykorzystywane jest następujące założenie – matematycznie efekt refrakcji atmosferycznej jest taki, jakby światło przebiegało po linii prostej, a Ziemia miała promień krzywizny równy r = R / (1 – k), gdzie R – promień Ziemi, k – współczynnik refrakcji.
To tyle z teorii. W praktyce współczynnik refrakcji można obliczyć za pomocą arkuszów kalkulacyjnych stworzonych przez Łukasza Wawrzyszko lub za pomocą opcji w programie heywhatsthat.com
Jakie wartości może przyjmować współczynnik refrakcji?
Refrakcja atmosferyczna, a fotografia długodystansowej.
Fotografia długodystansowa ma na celu uchwycenie obiektu z długiego dystansu. Zazwyczaj tego typu fotografie wykonywane są w warunkach standardowych bo takie występują najczęściej. Do uchwycenia obiektu z daleka często wystarczy „tylko” dobra widzialność i przejrzystość powietrza. Występowanie standardowej refrakcji (o współczynniku 0,13) jest wystarczające na przykład do obserwacji słowackich Tatr z dystansu powyżej 200 km z terenu Polski , ale także And z okolic Cordoby w Argentynie z dystansu 440 km.
Występują jednak obserwacje trudniejsze – ekstremalne dalekie obserwacje. Ekstremalne nie tylko ze względu na odległość od obserwowanego obiektu ale ze względu na trudność obserwacji – np. profil terenu i przeszkody. Przy takich obserwacjach dobra widzialność i przejrzystość powietrza nie wystarczą. Potrzebna jest zwiększona refrakcja atmosferyczna, która pozwoli na dostrzeżenie obiektu „schowanego” za horyzont. Na stronie dalekiewidoki.pl znajdziemy wiele takich zdjęć.
Teoretycznie lokalnie współczynnik refrakcji może przekroczyć wartość 1,0 -mamy wtedy do czynienia ze zjawiskiem superrefrakcji. W takim przypadku możliwe byłoby zobaczenie wszystkiego dowolnie daleko na Ziemi niezależnie od krzywizny Ziemi. Widoczne byłoby wszystko co wystawałoby powyżej warstwy w której superrefrakcja występuje. Oczywiście o ile pozwoliłyby na to warunki widzialnościowe takie jak przejrzystość powietrza (zapylenie, stężenie aerozoli itd).
Ekstremalne obserwacje Tatr z Polski.
Zacznijmy od przeglądu obserwacji Tatr. Tatry to najwyższe (maks. 2655 m n.p.m. ) pasmo górskie w Karpatach, a także najwyższe między Alpami a Uralem i Kaukazem. To pasmo górskie obserwowane było z Polski Centralnej i Wschodniej z dystansu ponad 230 km przy wymaganym współczynniku refrakcji powyżej 0,20.
Przejdźmy do przykładów. Zacznijmy od obserwacji słowackich Tatr z G. Kamieńskiej (Polska Centralna) z dystansu 232 km . Wymagany do obserwacji pojedynczego szczytu Tatr współczynnik refrakcji wynosi 0,19. Podczas obserwacji widocznej części Gerlacha wyniósł ok. 0,23.
Pełna relacja na stronie dalekiewidoki.pl . Obliczenia refrakcji dla tej obserwacji znajdziemy w artykule Dalekie Horyzonty.
Linia widzenia G. Kamieńsk – Gerlach. 232,1 km na mapie Google Maps.
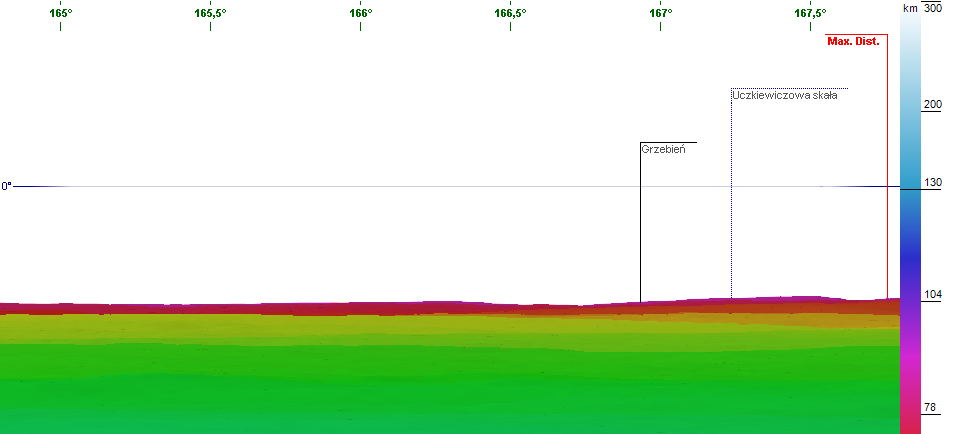

Kolejnym przykładem jest obserwacja Tatr z Wyżyny Lubelskiej z 233 km. Z puKolejnym przykładem jest obserwacja Tatr z Wyżyny Lubelskiej z 233 km. Z punktu w miejscowości Potok Wielki położonego tylko 245 m. n.p.m. współczynnik refrakcji atmosferycznej wymagany do obserwacji widocznej na zdjęciu części Zadniego Gerlacha (2616 m. n.p.m.) wyniósł ok. 0,22.

Obserwacje obiektów na niższych wysokościach i wpływ inwersji radiacyjnej.
Obserwacje obiektów na niższych wysokościach, gdzie linia widzenia jest blisko ziemi, są bardziej podatne na wpływ refrakcji niż obserwacje gór wysokich, gdzie światło pokonuje większą odległość nad ziemią. To związane jest z inwersją radiacyjną, która powstaje w cienkiej warstwie nad ziemią podczas bezchmurnej i bezwietrznej pogody, głównie w nocy. Ta warstwa ochładza się szybciej niż powietrze wyżej, co powoduje duży gradient temperatury i zwiększa współczynnik refrakcji.
Przejdźmy do przykładów takich obserwacji.
Warszawa z Gór Świętokrzyskich.
Obserwacją która obiegła ogólnopolskie media było zdjęcie stolicy Polski – Warszawy z Gór Świętokrzyskich z odległości ponad 150 km.
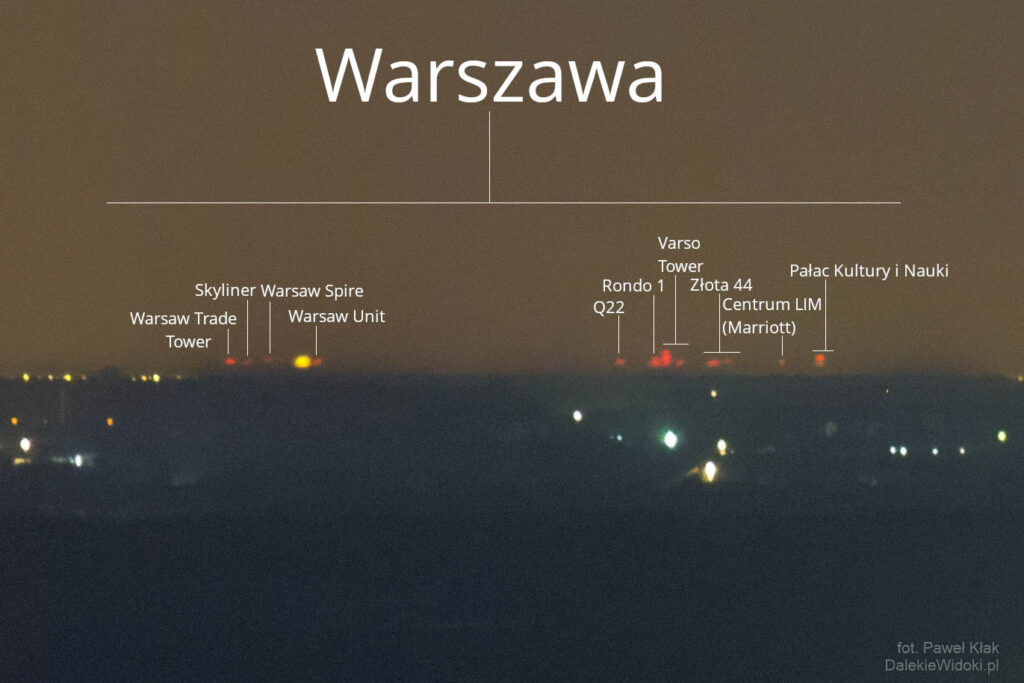
Zmieniająca się refrakcja atmosferyczna w czasie powodowała pojawianie się i zanikanie warszawskich wieżowców nad horyzontem.

W szczytowym momencie refrakcja była tak silna , że widoczny był na zdjęciu budynek – Centrum LIM – wymagało to współczynnika refrakcji 0,44! , czyli światło musiało załamać się aż 3-krotnie silniej niż standardowo. Ze względu na niejednorodność atmosfery mowa o uśrednionych współczynnikach dla całego dystansu obserwacji.
Aby w standardowych warunkach (wsp. refrakcji ~ 0,14) był widoczny szczyt masztu Centrum LIM, budynek ten musiałby być wyższy o ok. 190 metrów albo należałoby się wznieść ponad 360 m ponad miejscem obserwacji.
Co istotne silną refrakcję i inwersję radiacyjną wymaganą do tej obserwacji potwierdzają oficjalne dane dostępne ze stacji Legionowo o godzinie 2:00 28 maja 2023 , które pochodzą z balonu meteorologicznego wykorzystywanego do sondowania atmosfery .
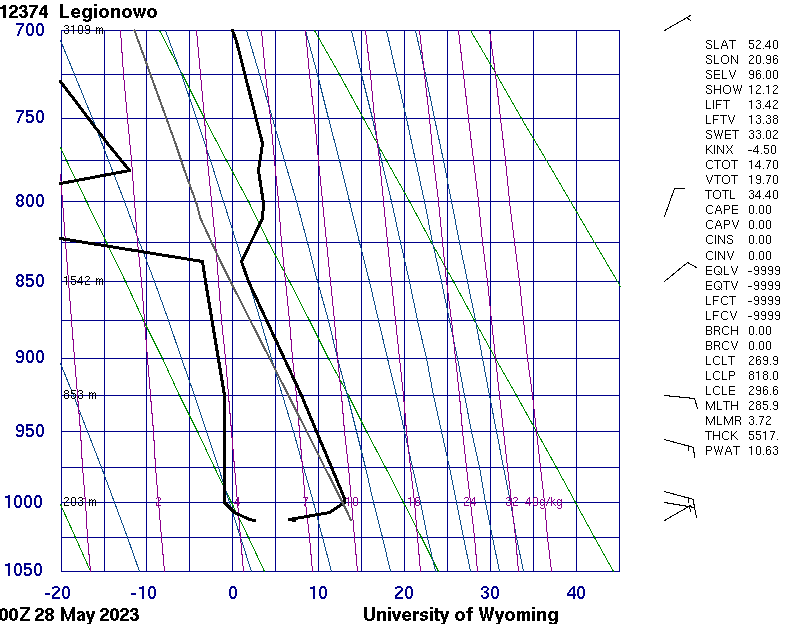
W Legionowie wystąpiła inwersja temperatury na wysokościach od 104 do 203 metrów nad poziomem morza, co stanowi około 10 do 110 metrów nad powierzchnią ziemi (prawdopodobnie sięgała nieco wyżej, ponieważ temperatura była identyczna na wysokościach 203 i 228 metrów nad poziomem morza). Nie posiadamy danych z trasy Warszawa – Łysa Góra, więc niemożliwe jest dokładne określenie rozkładu tego współczynnika na całej linii obserwacji. Niemniej jednak warunki pogodowe były podobne, więc prawdopodobnie także tam występowała inwersja temperatury. Linia widzenia tylko na części trasy przechodziła przez warstwę inwersji, dlatego średni współczynnik refrakcji jest znacznie niższy niż jego maksymalne wartości. Najniższym widocznym obiektem w Warszawie na zdjęciach jest światło na maszcie na budynku Centrum LIM, którego szczyt sięga 295 metrów nad poziomem morza.
Za pomocą specjalnego oprogramowania, które analizuje, jak światło rozchodzi się w atmosferze przy uwzględnieniu konkretnego pionowego profilu temperatury, jesteśmy w stanie określić linię widzenia w danym zestawieniu warunków.
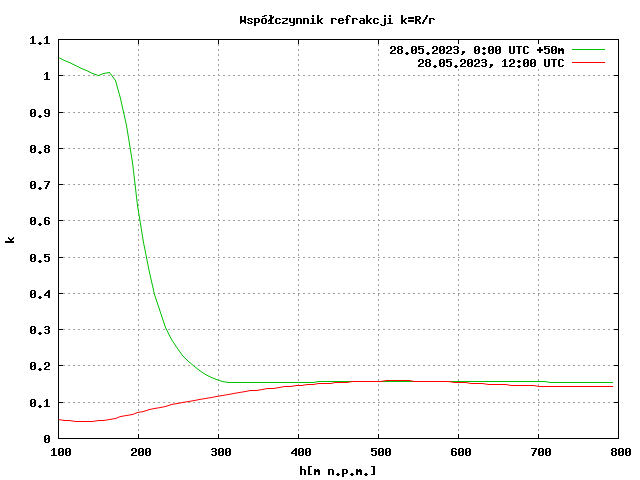
Przedstawione poniżej wykresy zostały przygotowane przez doktora habilitowanego Krzysztofa Strasburgera na podstawie pomiarów przeprowadzonych w Legionowie. Szczegółowy opis można znaleźć na jego stronie internetowej.
Warszawa z okolic Łodzi.
Inną ciekawą obserwacją są zdjęcia Warszawy z okolic Łodzi przestawione są w artykule. Przeanlizujmy tą obserwację pod kątem niestandardowej refrakcji atmosferycznej.

Kilka minut później zmieniająca się refrakcja pokazała swoje piękno. Pojawiło się znacznie więcej obiektów Warszawy.

Na horyzoncie ukazało się kilkanaście wieżowców Śródmieścia i Woli: Warsaw Trade Tower, Warsaw Spire, Spektrum Tower, Łucka City, Generation Park, Mennica Legacy Tower, Skysawa, Unit, Skyliner, Rondo 1, The Warsaw Hub, Złota 44, Pałac Kultury i Nauki, Varso Tower, Centrum LIM (Marriott), Chałubińskiego 8 ale także obiekty dużo niższe takie jak wieża kontroli (TWR) lotniska Chopina w Warszawie.
Przebieg linii widzenia Kalenice – Warszawa.
Obserwator : Kalenice, woj.łódzkie, z punktu przy lesie w okolicach autostrady A2 , wys. 166 m. n.p.m. 51°57’47.7″N 19°51’22.7″E
Obserwowany obiekt: wieża kontroli (TWR) lotniska Chopina w Warszawie – wys. 153 m n.p.m. 52°09’44.6″N 20°57’34.5″E
Odległość: 78,6 km
Poniższe ilustracje przedstawiają przebieg linii widzenia Warszawy (wieża kontroli lotniska Chopina) z Kalenic. k Łodzi i zostały wykonane za pomocą programu heywhatsthat.com.
Pokazują one, jak ukształtowanie terenu na linii obserwacji zasłaniałoby widok, gdyby światło rozchodziło się po linii prostej, a także przy refrakcji atmosferycznej o standardowej wielkości.
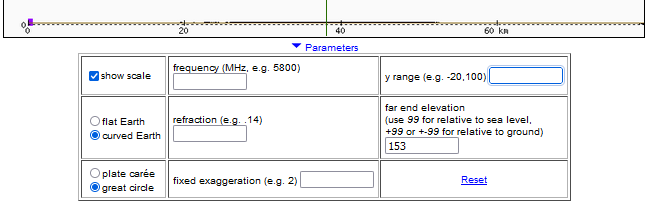
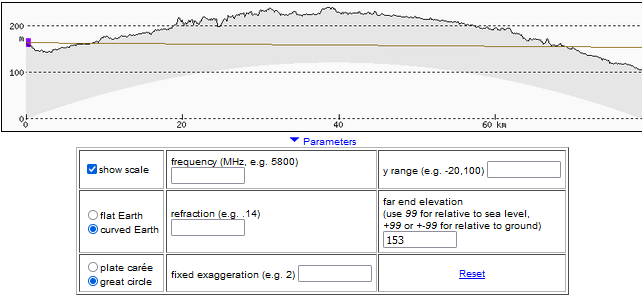
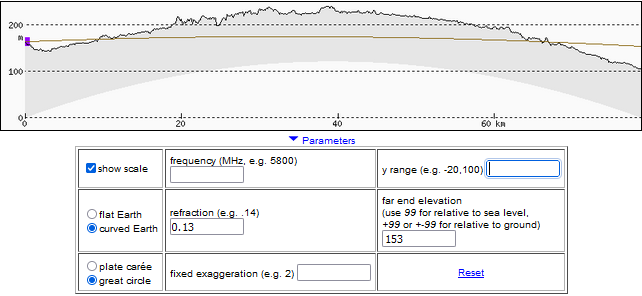
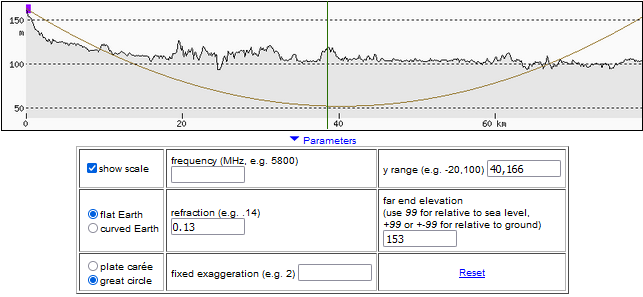
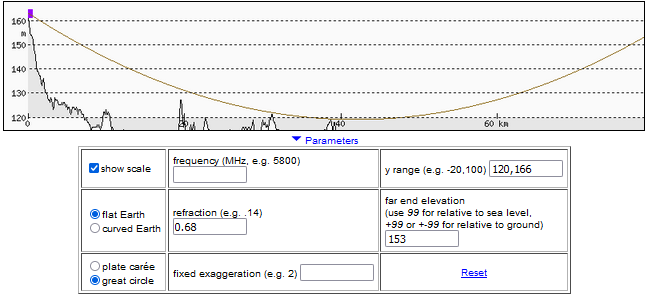
Wyznaczanie minimalnego współczynnika refrakcji wymaganego do obserwacji
Czy można dokładnie policzyć, jak bardzo musi się zwiększyć refrakcja, żeby widoczność była możliwa? Tak, ale musimy pamiętać o pewnych ograniczeniach, jakimi obarczone są te analizy. Przede wszystkim powietrze jest niejednorodne i refrakcja zmienia się w przestrzeni i czasie. Jej wielkość określamy za pomocą współczynnika refrakcji, zdefiniowanego jako iloraz promienia krzywizny Ziemi i krzywizny łuku, po którym biegną promienie światła. Nie znamy jego dokładnych wartości w każdym punkcie na linii obserwacji, musimy więc przyjąć uproszczenie zakładające jego stałą wartość – jest to jego średnia (efektywna) wartość z całej linii obserwacji.
Wykorzystajmy funkcjonalność programu heywhatsthat.com. Potrzebujemy jednak kilka istotnych danych na temat obserwacji.
Wyliczenie współczynnika refrakcji.
Na zdjęciu widać światła wieży kontroli (TWR) lotniska Chopina w Warszawie minimalnie wystające nad horyzontem. Znając ich wysokość (153 m n.p.m.), wysokość miejsca obserwacji (166 m n.p.m.) oraz wysokość drzew, nad którymi je widać, można oszacować, jak duża była refrakcja atmosferyczna. Lokalizację drzew i ich wysokość odczytujemy z modelu NMPT w Geoportalu, korzystając z profilu terenu na heywhatsthat.com (opis metody) – wynosi ona ok. 130-140 m n.p.m dla drzew Puszczy Bolimowskiej w okolicy Żyradowa i punktu 52,062318 20,396667. Dla obliczeń przyjmijmy wartość 135 m.n.p.m.
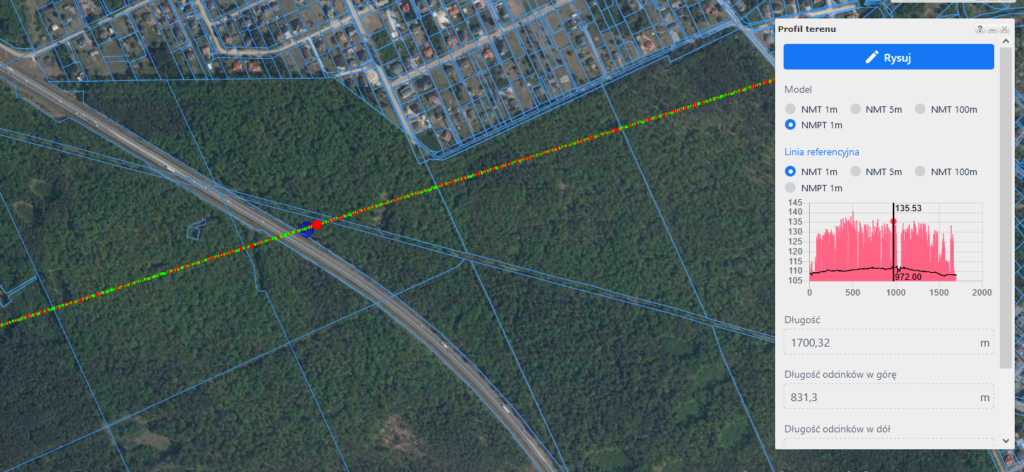
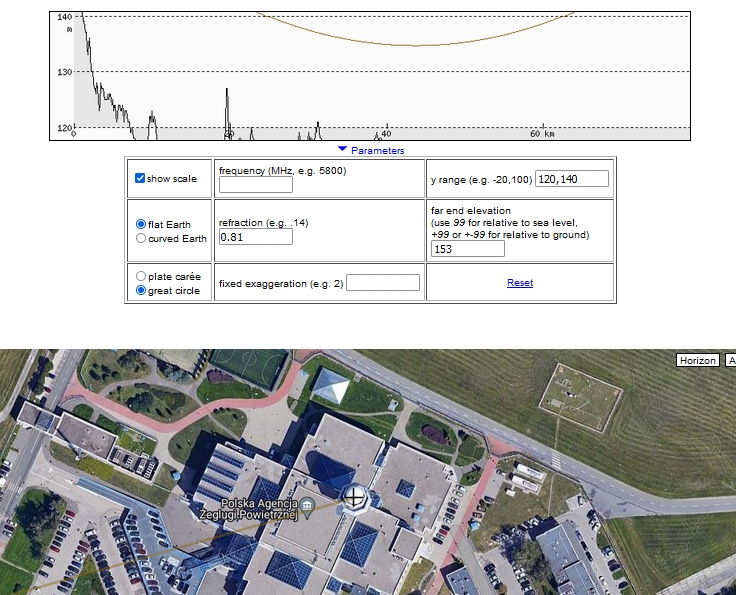
Na profilu terenu w heywhatsthat.com linia widzenia przechodzi w lokalizacji tych drzew na wysokości ok. 135 m n.p.m., gdy współczynnik refrakcji wynosi ok. 0,81. Podobne wartości wynikają także z analizy widoczności innych budynków.
Sprawdźmy teraz współczynnik refrakcji wymagany do obserwacji Marynarska Business Park.
Można go obliczyć za pomocą arkusza kalkulacyjnego, w którym podajemy wysokość n.p.m. miejsca obserwacji, obserwowanego szczytu oraz najdalszego punktu widocznego przed tym szczytem, a także odległość z miejsca obserwacji do obu tych punktów.
Arkusz ten wykorzystuje fakt, iż przy minimalnej refrakcji zapewniającej widoczność, wszystkie trzy wymienione punkty leżą na wspólnym okręgu – obliczenia polegają na znalezieniu jego promienia, a następnie podzieleniu przez niego promienia Ziemi. Szczegółowy opis wykorzystywanych w nim równań znajduje się na stronie Obliczenia.
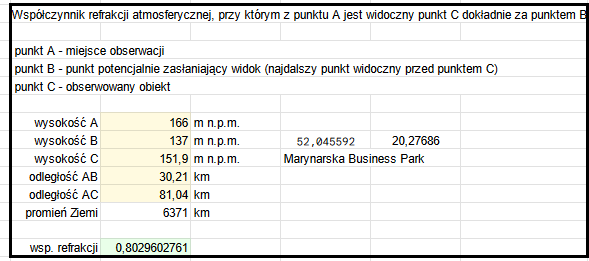
Współczynnik refrakcji wymagany do obserwacji budynku Marynarska Business Park wynosi ok. 0,80.
Uśredniony współczynnik refrakcji nie oddaje oczywiście w pełni dynamiki refrakcji na całej linii widzenia. Refrakcja jest zmienna w czasie na różnej wysokości. Niewątpliwie na pewnym dystansie obserwacji współczynnik tej przekroczył wartość 1. Refrakcji nie można jednak „zamknąć” w jednej wartości dla całej linii widzenia. Uśredniony współczynnik refrakcji natomiast daje pewien pogląd na trudność obserwacji oraz siłę z jaką musi zadziałać refrakcja by obiekt mógł „wynurzyć się” zza horyzontu i być widocznym.
Mieliśmy do czynienia z refrakcją radiacyjną. Światło przemierzając drogę w niejednorodnej atmosferze ugięło się silnie w skutek „zanurzenia się” w przygruntowej warstwie inwersyjnej. . We wspomnianej warstwie zapewne doszło do zjawiska superrefrakcji – współczynnik refrakcji mógł mieć w niej wartość powyżej 1. W takim przypadku teoretycznie możliwe było zobaczenie wszystkiego dowolnie daleko na Ziemi , co wystawało powyżej tej warstwy. Oczywiście o ile pozwoliłaby na to warunki widzialnościowe takie jak przejrzystość powietrza, zapylenie oraz stężenie aerozoli. W rzeczywistości sytuacja by zajrzeć dowolnie daleko nie jest tak optymistyczna. Po pierwsze, światło ulega rozproszeniu na aerozolach, zawsze obecnych w pewnym stopniu, oraz na cząstkach gazów tworzących powietrze. Po drugie, warstwa powietrza o tak interesujących właściwościach nie jest jednorodna i ma ograniczony zasięg.
Efektem silnego załamania była deformacja obrazu wieżowców tj. spłaszczenie obiektów oraz dynamiczne zmiany ich rozmiarów w czasie. Światła wieżowców położone na różnych wysokościach nad poziomem morza na kilku zdjęciach wyglądają jakby „leżały” na jednym poziomie. Gwałtowne zmiany temperatury i częściowo ciśnienia atmosferycznego związane ze zbliżającym się frontem oraz związane z tym dynamiczne zmiany grubości warstwy inwersyjnej oraz jej „falowanie” doprowadziły do bardzo intensywnych zmian obrazu obserwowanych obiektów oraz ich rozmiarów kątowych w stosunkowo krótkim czasie.
Co istotne inwersję radiacyjną i zwiększoną refrakcję wymaganą do tego typu obserwacji potwierdzają oficjalne dane dostępne ze stacji z pobliskiego Legionowo o godzinie 2:00 27 czerwca 2023 , czyli 3h po obserwacji. Dane pochodzą z balonu meteorologicznego wykorzystywanego do sondowania atmosfery .
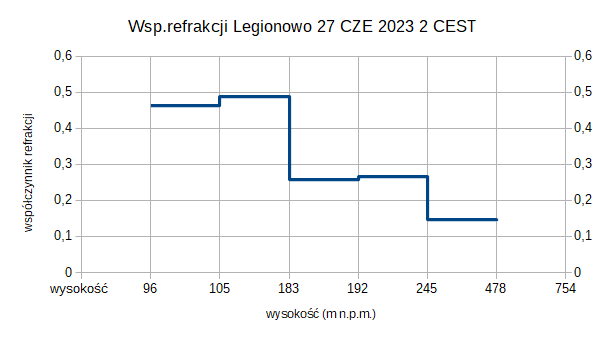
Inwersja temperatury w Legionowie wystąpiła w zakresie wysokości 96 – 245 m n.p.m. czyli maksymalnie ok.160 m nad ziemią i uśredniona wartość nie przekroczyłą 0,5.
Odstęp 3 godzinny to dosyć duży okres czasu i to tłumaczy różnicę wartości refrakcji wyliczonej dla obiektów widocznych z Kalenic z tą wyliczoną dla Legionowa . Warstwa inwersyjna mogła zmienić się nawet w ciągu kilku minut , co zresztą było widoczne na zdjęciach. Nie da się określić dokładnego rozkładu tego współczynnika na linii obserwacji, gdyż nie są to dane z linii Warszawa – Kalenice. To co możemy wyciągnąć istotnego z danych z Legionowa to nie siła i wartość ale sam fakt pojawienia się inwersji w okolicy.

