[210 km] Tatry z okolic Skarżyska – Kamiennej.

Zdjęcia przedstawiają: Tatry Zachodnie
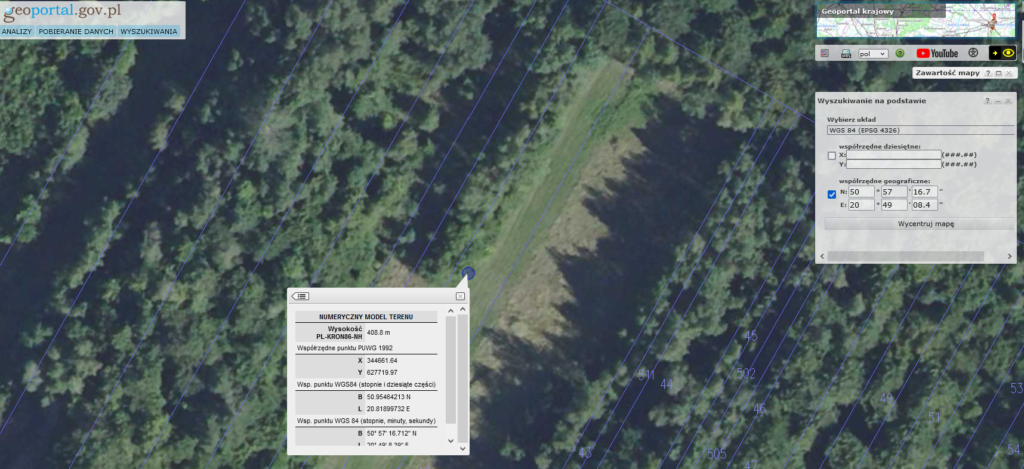
Miejsce:  Klonów, powiat skarżyski , woj. świętokrzyskie 50°57’16.7″N 20°49’08.4″E
Wysokość obserwatora: 407 m. n.p.m.
Odległość:  Zadnia Kopa – 209,7 km, Bystra 208,4 km, Starorobociański 207,8 km,  Jakubina 208,9 km, Jarząbczy 208,6 km, Krzesanica 202,2 km
Czas: 29.12.2022
Autor: Paweł Kłak
Symulacja z Ulricha (nie uwzględnia lasów) –  RC0.13   RC0.15 RC0.17 RC0.18

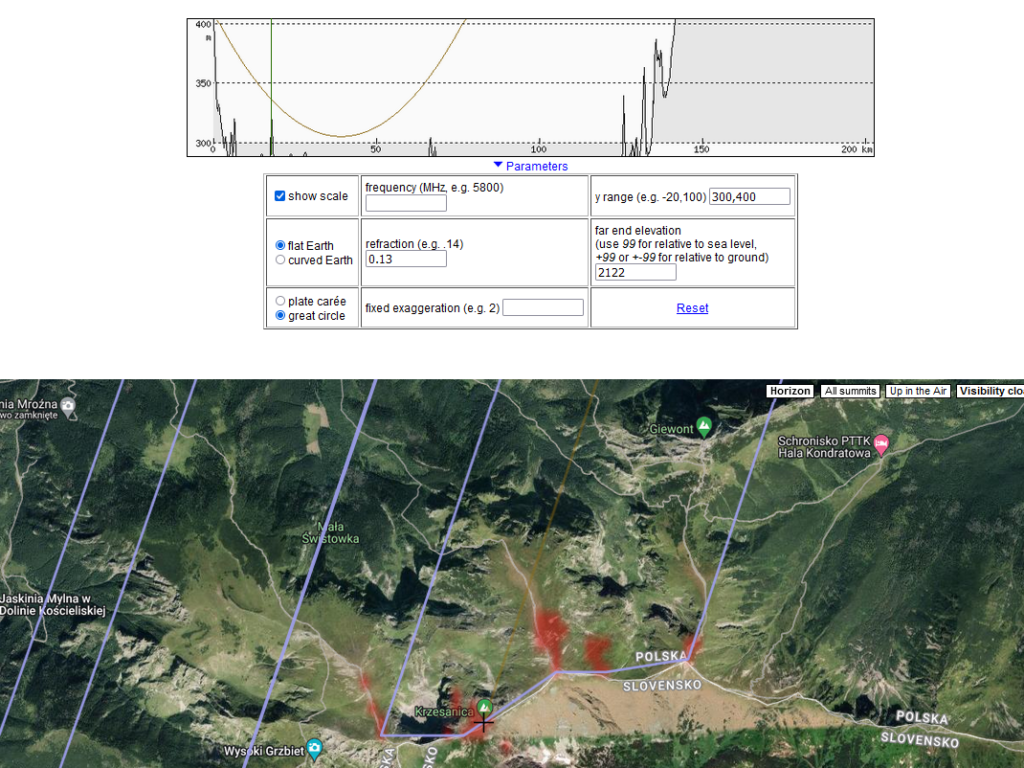
Linia Klonów – Zadnia Kopa na Mapie Google.

Wyznaczenie  średniego (efektywnego) współczynnika refrakcji dla obserwacji szczytu Krzesanicy.

Oznaczenia:
punkt A – punkt, z którego wykonano obserwację
punkt B – punkt na linii obserwacji potencjalnie zasłaniający widok
punkt C – obserwowany punkt – szczyt Krzesanica

Etap 1. Wyznaczenie współrzędnych oraz wysokości punktów A i C.

Etap 2. Wyznaczenie współrzędnych oraz wysokości punktu B.

Etap 3. Wyznaczenie odległości pomiędzy punktami A i B  oraz A i C.

Etap 4. Podstawienie danych do arkusza – otrzymujemy minimalny współczynnik refrakcji wymagany dla obserwacji wierzchołka szczytu z uwzględnieniem przeszkód terenowych .

Etap 5 – obliczenie efektywnego współczynnika refrakcji dla widocznej części szczytu Krzesanica

Etap 1. Wyznaczenie współrzędnych oraz wysokości punktów A i C.

Krok 1 : Do wyznaczenia współrzędnych punktów A oraz C wykorzystujemy funkcjonalności serwisów np. Mapy Google, Geoportal, mapy.cz.

• Punkt A – punkt obserwatora –  współrzędne pobieramy np. z Map Google – 50.954639, 20.819000    50°57’16.7″N 20°49’08.4″E
• Punkt C – obserwowany szczyt – Krzesanica  , współrzędne pobieramy np. za pomocą strony mapy.cz https://pl.mapy.cz/s/negadobomu 49°13’53.993″N, 19°54’34.170″E

Krok 2:  Wyznaczanie wysokości  punktów A i C.

Punkt A :   W serwisie www.geoportal.gov.pl, w menu „Wyszukiwania”, wybieramy  „Wyszukiwanie na podstawie współrzędnych”. Kolejnym krokiem jest wybranie przycisku „Wycentruj mapę”. Wynikiem wyszukiwania jest niebieski punkt reprezentujący wskazane współrzędne oraz przesunięcie mapy –  wycentrowanie jej w wyszukiwanym miejscu.

Klikamy na punkt lewym klawiszem myszki i wybieramy WMS: Wyznaczanie wysokości. Pojawia nam się okno zatytułowane  Numeryczny Modelem Terenu.

Odczytujemy wartość z pola Wysokość PL-KRON86-NH –  jest to wartość 408,8 m n.p.m.

Punkt C : obserwowany szczyt to Krzesanica  –  pobieramy wysokość z ogólnodostępnych danych w internecie.  Najlepiej porównać dane z kilku serwisów np. z  Wikipedii https://pl.wikipedia.org/wiki/Krzesanica lub ze strony mapy.cz https://pl.mapy.cz/s/negadobomu . W obu przypadkach podana wysokość to 2122 m.n.p.m. Uznajemy tą wartość za wiarygodną.

Mamy, więc pierwsze dane – współrzędne punktu A,C oraz ich wysokości.

Etap 2. Wyznaczenie współrzędnych oraz wysokości punktu B.

Przechodzimy do najtrudniejszej i najbardziej czasochłonnego etapu  –  wyznaczenie punktu B  – czyli punktu na linii obserwacji potencjalnie zasłaniającego widok.

Krok 1.  Korzystamy ze strony https://www.heywhatsthat.com/  i wypełniamy pola:

• w polu numer 1 podajemy współrzędne obserwatora czyli te z punktu A : 50.954639, 20.819000
• w polu numer  3 podajemy  wysokość obserwatora – wpisujemy ręcznie wartość którą pobraliśmy dla punktu A w  Etapie 1 Krok 2  –  408,8 m n.p.m. –  zaokrąglamy do 409.   Jeśli zostawimy to pole puste , program pobierze wysokość z modelu terenu wykorzystywanego przez Mapy Google (czasem różni się o kilka metrów, w tym przypadku pobrał błędną wartość 413 m)
• w polu numer  4 podajemy nazwę projektu – może to  być dowolna nazwa
• klikamy Submit request
• pojawia nam się wygenerowana mapa widoczności – link dla tej obserwacji

  

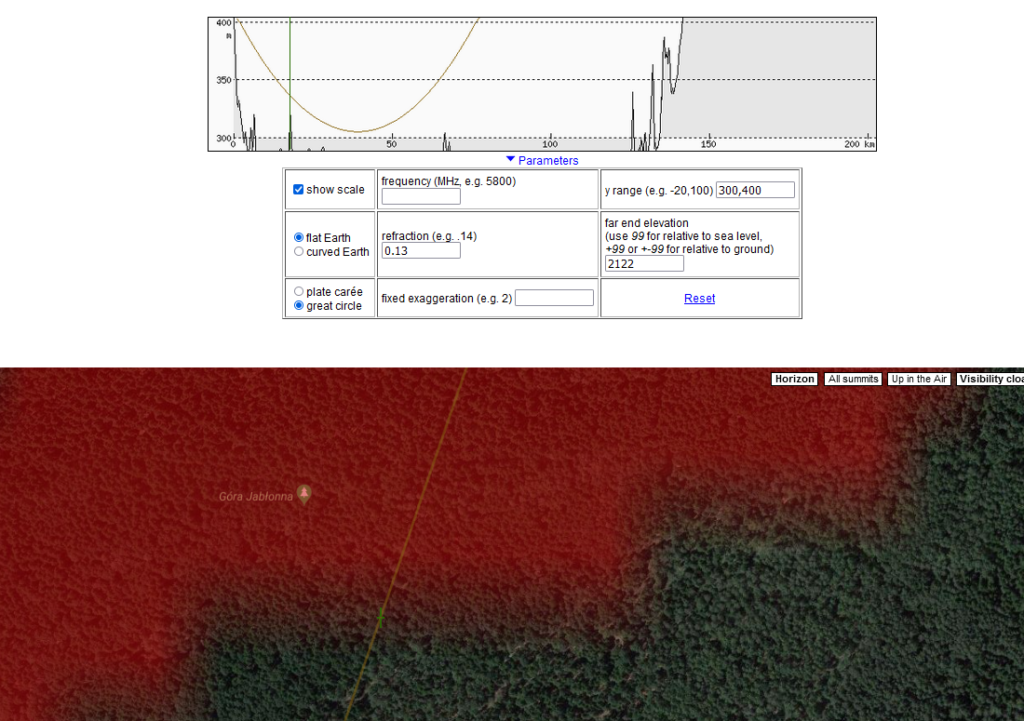
• po wygenerowaniu mapy , szukamy na niej analizowany szczyt w tym przypadku Krzesanicę i klikamy w niego.  Pojawia nam się jasnobrązowa linia przebiegu światła pomiędzy obserwatorem a Krzesanicą naniesiona na schemat z profilem terenu na całym dystansie obserwacji. Powyżej mapy klikamy Parameteres i uzupełniamy dane . Sprawdźmy standardowe warunki – w polu „refraction” wpisujemy wartość 0.13.  w polu „Far and elevation” – wpisujemy wysokość szczytu Krzesanicy – 2122  Obserwujemy cały czas linię przebiegu światła , widzimy, że dla współczynnika  0.13 linia widzenia omija wszystkie przeszkody.  Wygląda to dobrze, ale czy tak jest w rzeczywistości?  Musimy to sprawdzić.

• Program www.heywhatsthat.com korzysta z modelu terenu nie uwzględniającego przeszkód takich jak lasy. By mieć pewność , że standardowe warunki refrakcyjne 0.13 wystarczą szukamy miejsca, w którym linia widzenia jest „najbliżej” terenu. Korzystamy z  pola „y range”  – tutaj korygujemy wartość  w celu „zbliżenia” i łatwiejszego znalezienia potencjalnej przeszkody. Wpisaliśmy wartość 300,400 widzimy znaczne przybliżenie.  Klikamy na „pole profilu”  w miejscu, gdzie linia światła jest najbliżej, wtedy pojawia się zielona pionowa kreska, a na mapie pojawia się punkt w terenie w pobliżu Góry Jabłonnej. Widzimy , że teren porastają lasy zapewne sosnowe, a takie potrafią mieć nawet 30m wysokości. Heywhatsthat nie uwzględnia ich w symulacji.  Dlatego musimy punkt znaleźć i ręcznie sprawdzić jego rzeczywistą wysokość z uwzględnieniem lasów. Punkt oznaczony jest zielonym krzyżykiem. Musimy odnaleźć jego współrzędne na Mapie Google. Przechodzimy do kolejnego kroku.

Krok 2.  Szukamy punktu B na Mapie Google i odnajdujemy współrzędne oraz wyznaczamy wysokość z uwzględnieniem lasów.

• przechodzimy na Mapy Google i szukamy tego punktu  (w heyu oznaczony zielonym krzyżykiem) . Odnajdujemy go tu  https://goo.gl/maps/frEqnfHcW8Df59rY6 . Mamy punkt B –  ma  on współrzędne 50°48’13.0″N 20°44’11.4″E 50.803610, 20.736490
• pozostało nam wyznaczanie wysokości punktu B  (czyli teren+ las) za pomocą Geoportalu i modelu NMPT (Numeryczny Model Pokrycia Terenu).

W serwisie www.geoportal.gov.pl, w menu „Wyszukiwania”, wybieramy  „Wyszukiwanie na podstawie współrzędnych”. Kolejnym krokiem jest wybranie przycisku „Wycentruj mapę”. Wynikiem wyszukiwania jest niebieski punkt reprezentujący wskazane współrzędne oraz przesunięcie mapy –  wycentrowanie jej w wyszukiwanym miejscu.

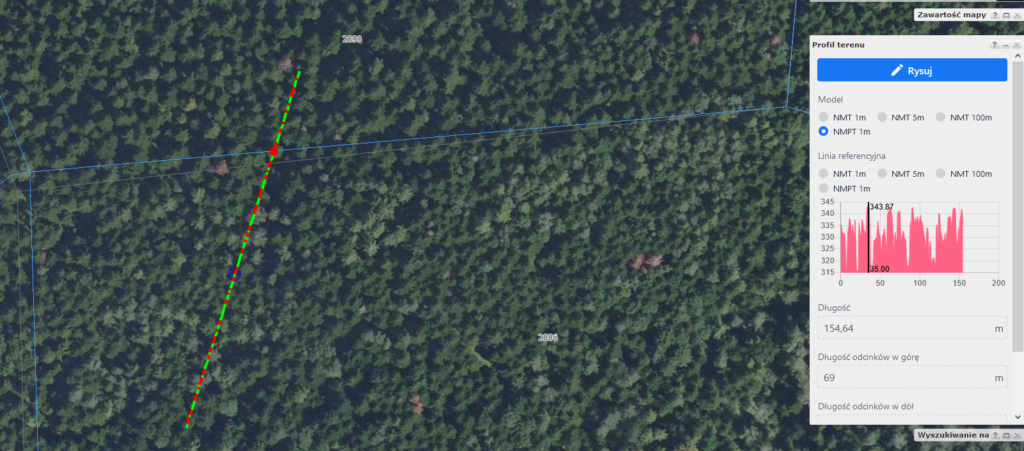
Kolejnym krokiem jest wybór z menu Analizy – Numeryczny Model Terenu -> Profil terenu.

• rysujemy linię przechodzącą przez niebieski punkt – linia powinna być maksymalnie zbliżona do linii obserwacji w  Heywhatsthat – można znaleźć charakterystyczne punkty zaczepienia – np. drzewa , budynki itp
• na wygenerowanym w prawym okienku  strony  wyświetla nam się  profil wysokościowy   – ma być wybrany model „NMPT 1 m” ( w tym kroku interesuje nas wysokość z uwzględnieniem przeszkód czyli  wysokość terenu + drzewa)
• odczytujemy najwyższą wartość wysokości dla linii przechodzącej przez punkt B  – 344 m.n.p.n. 
• w tym momencie mamy już wszystkie punkty A, B, C oraz ich wysokości. Pozostaje nam przejść do etapu 3 – wyznaczenie odległości między punktami

Etap 3. Wyznaczenie odległości pomiędzy punktami A i B  oraz A i C.

Krok 1 : mając wyznaczone wcześniej współrzędne punktów A , B , C korzystamy z dostępnych w sieci kalkulatorów np. polskiego kalkulatora PIAST (Platforma Informatyczna Analiz Systemów Telekomunikacyjnych )  link opcja -Wyznaczanie odległości i azymutu między dwoma punktami. Można też korzystać z kalkulatora Eda Williamsa.

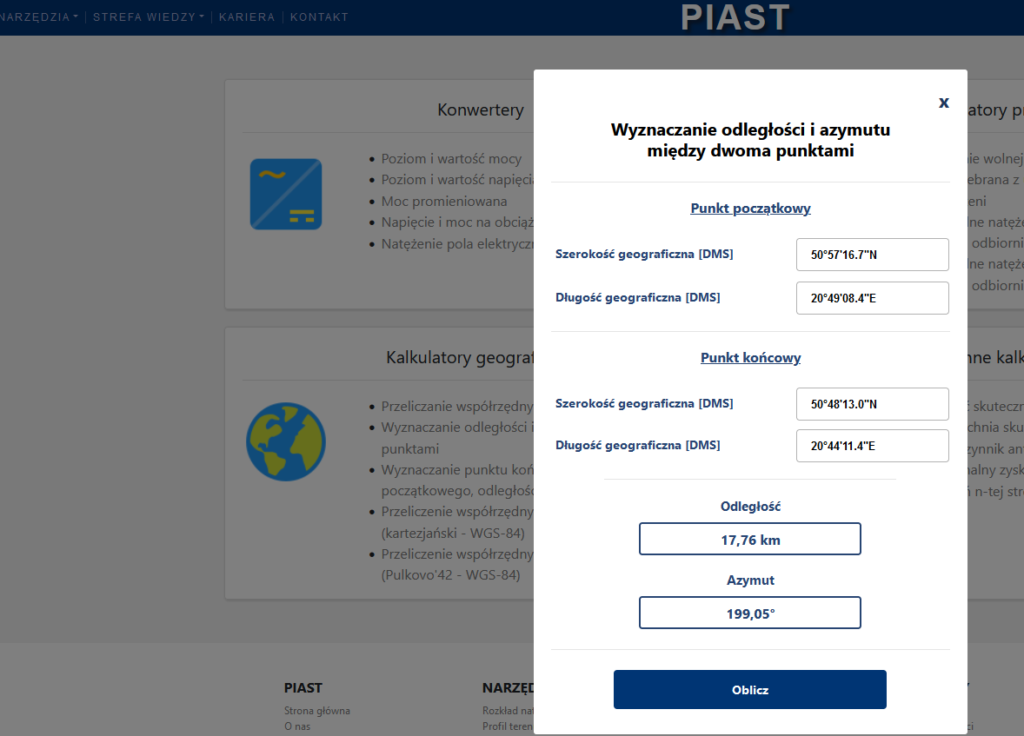
Krok 2: Wyznaczone odległości : pomiędzy punktem A i B to 17,76 km , a między punktami A i C to 202,26 km.

Etap 4. Podstawienie danych do arkusza – otrzymujemy minimalny współczynnik refrakcji wymagany dla obserwacji wierzchołka szczytu z uwzględnieniem przeszkód terenowych .

Zebraliśmy już podstawowe dane – współrzędne punktów , wysokość punktów oraz odległości między nimi.  Teraz pora na wstawienie ich do arkusza autorstwa Łukasza Wawrzyszki z dalekiehoryzonty.pl.

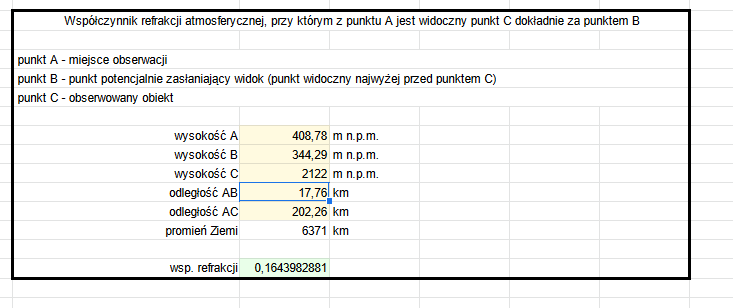
Po wypełnieniu  wymaganych pól otrzymujemy minimalny współczynnik refrakcji wymagany dla  obserwacji Krzesanicy z punktu 50°57’16.7″N 20°49’08.4″E z uwzględnieniem zalesionej przeszkody w punkcie B (tj. lasów na Górze Jabłonnej).  Otrzymany wynik to ok. 0,164.  Co nam to mówi? Pierwszy wniosek to taki, że szczytu nie zobaczylibyśmy w standardowych warunkach refrakcyjnych (współczynnik refrakcji – 0,13-0,14 – przypomnijmy sobie, że heywhatsthat pokazywał,że wystarczy 0.13 ).  Warto zauważyć , że współczynnik 0,164  jest  to wartość minimalna,  wymagana by ujrzeć na zdjęciu sam wierzchołek Krzesanicy. Na zdjęciach widzimy znacznie więcej niż sam wierzchołek.   Efektywny współczynnik był, więc  dużo wyższy. Jak obliczyć ten efektywny? Przejdźmy do etapu 5.

Etap 5 – obliczenie efektywnego współczynnika refrakcji dla widocznej części szczytu Krzesanica

Krok 1: Wykorzystanie kalkulatora pola widzenia obiektywu –  wybieramy rozmiar matrycy (APS-C Canon) , ogniskową (500mm) i rodzaju wykorzystywanego obiektywu którym zrobiono analizowane zdjęcie. Podajemy również  odległość od  fotografowanego szczytu – w naszym przypadku do szczytu Krzesanicy jest 202,26 km czyli 202260 metrów.

• Interesuje nas pole widzenia: wartość w pionie to 6067,8 m.

Krok 2 : Analiza zdjęcia w programie GIMP.

• Sprawdzamy wymiary zdjęcia w programie GIMP : wysokość 3456 pikseli.

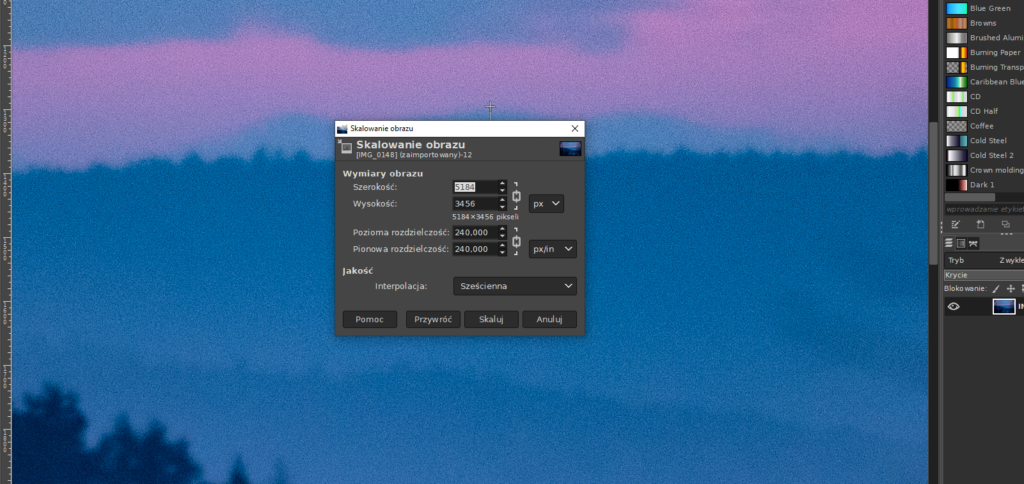
• mierzymy jaka część szczytu Krzesanicy jest widoczna – mierzymy piksele  Gimp – Narzędzie – Miarka (Shift +M)  – 70 pikseli

• 

• teraz pora na prostą matematykę.  Skorzystamy ze wzoru – widoczna część szczytu w pikselach na zdjęciu  / wysokość zdjęcia w pikselach * wartość w pionie pola widzenia .
• Podstawiamy wartości 70/3456*6067,8 m = 122,90 m – tak część szczytu Krzesanicy jest widoczna na zdjęciu.

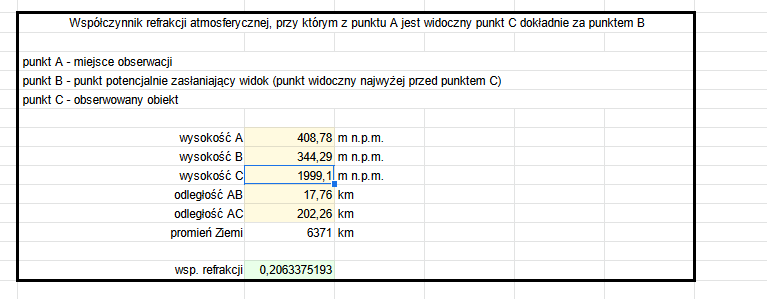
Krok 3: wracamy do refrakcji i arkusza. Skoro widzimy 122,90 m szczytu to w arkuszu w polu wysokość C musimy podać wartość, która jest różnicą pomiędzy wysokością szczytu 2122 a widoczną częścią – 122,90 czyli 2122-122,90 = 1999,1. Resztę danych mieliśmy wcześniej przygotowane. Efektywny uśredniony współczynnik refrakcji dla obserwacji  widocznej części Krzesanicy z Klonowa wyniósł w momencie obserwacji 0,206 .

Podobną analizę można wykonać dla pozostałych szczytów.